4次元超立方体
阿修羅の顔はなぜ3つあり、ケルビムの顔はなぜ4つあるのか~4次元の幾何学を使って神仏の姿を説明してみる~5.-1 4次元立方体(超方体、正八胞体)の作り方 → ”立方体を4次元方向に動かして作る” それでは、いよいよ正八胞体(4次元立方体)を作ってみましょう。.

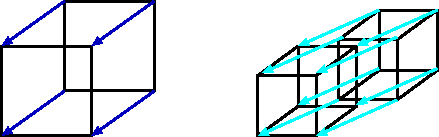
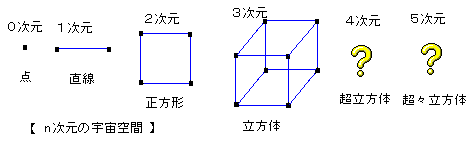
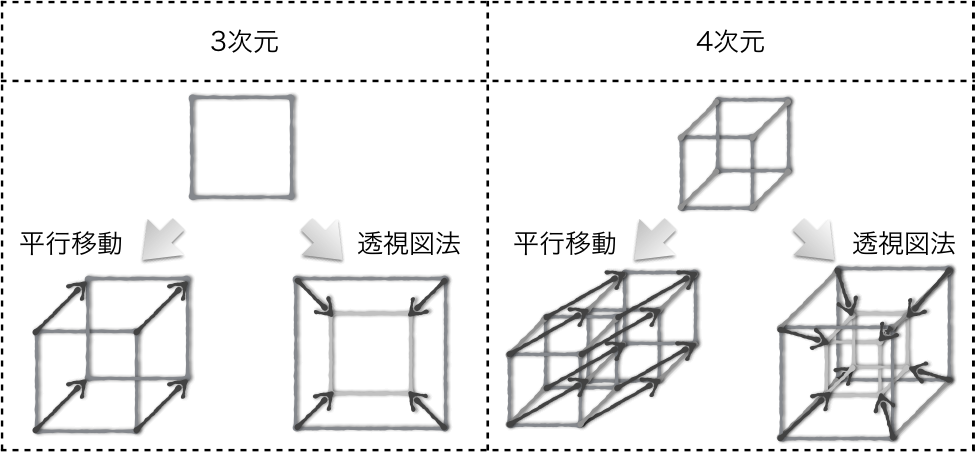
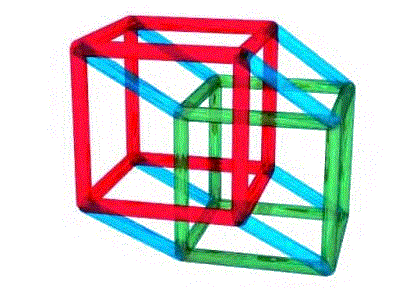
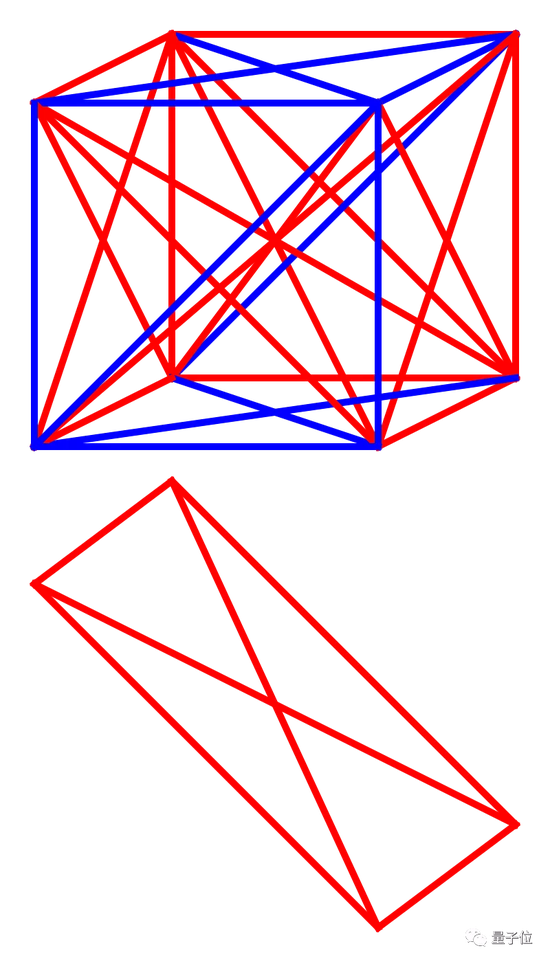
4次元超立方体. 3次元→4次元 3次元の赤い立体を、赤い点から出ている赤い線全てに垂直な方向に、 単位長さだけ平行に青い立体まで移動します。 赤い立体と青い立体と面の軌跡で囲まれる超立方体が描けます。 超立方体が8個の立方体に囲まれている様子が見える. 超立方体(hypercube)とは、2次元の正方形、3次元の立方体、4次元の正八胞体を各次元に一般化した正多胞体である。なお、0次元超立方体は点、1次元超立方体は線分である。(wikiから引用) 4次元超立方体の例(wiki引用) 性質 性質としてwikiに述べてある事例を述べる。. つまり4次元だ。至聖所(神の臨在の場)は3次元立方体(完全立体)だったが、キリスト(神の臨在そのもの)は四次元の立方体 4) 新エルサレムは一辺12,000スタジオンの立方体。それは小羊の花嫁であり、神の臨在そのものだから神殿もなく、それ自体が神.
超立方体(ちょうりっぽうたい、hypercube)とは、2次元の正方形、3次元の立方体、4次元の正八胞体を各次元に一般化した正多胞体である。 なお、0次元超立方体は点、1次元超立方体は線分である。 正測体(せいそくたい)、γ体(ガンマたい)とも言い、n 次元超立方体を と書く。. 超立方体(ちょうりっぽうたい、hypercube)とは、2次元の正方形、3次元の立方体、4次元の正八胞体を各次元に一般化した正多胞体である。 なお、0次元超立方体は点、1次元超立方体は線分である。 正測体(せいそくたい)、γ体(ガンマたい)とも言い、n 次元超立方体を と書く。. 数学・算数 - 4次元の超立体の検証 よろしくお願いします。 4次元空間における、超立体についてよく知りたいのですが、捉え方がまだよくわかりません。 私の読んだ某雑誌では、 0次元の点は端がないの.
4次元超 立方体ともいう。2つの立方体を平行に、対応する頂点が立方体に対して垂直に、かつ距離が1辺の長さになるように配置し、線で結んだもの。立方体を8個貼り合わせたものであり、32本の辺、24枚の正方形をもつ。 正十六胞体 正八面体の4次元. 5 次元空間の完全な知覚体からは3 次元空間にあるすべてのものの内部を見ることも、3 次元空間のある対象を360 度の角度から 時にみることもできる。超意識体は4 次元時空 連続体の時間と空間の制約(距離による分離)を超えている。5 次元界は我々の4. D=2次元になると,状態数は3×3=9個になります. また,d=3次元になると,立方体を考えれば状態数は3×3×3=27個になります(上の図の個数を考えるのが面倒なので立方体にしました). つまり,次元 に対して状態の数はざっくり で増加することになります..
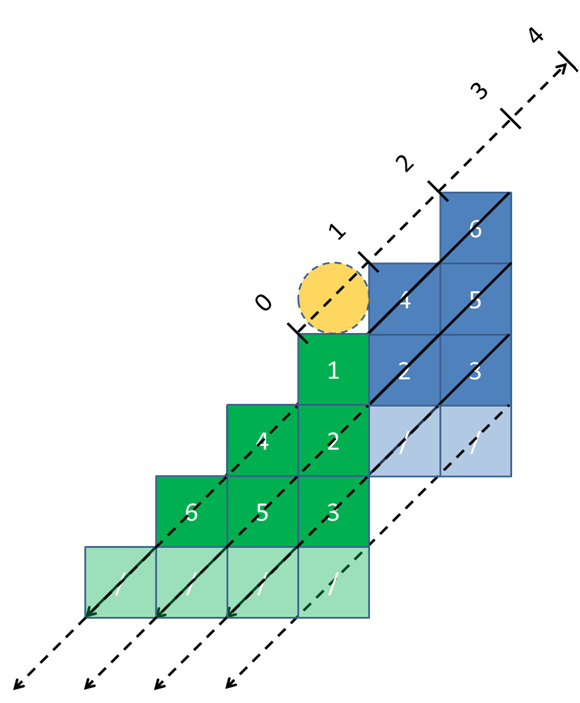
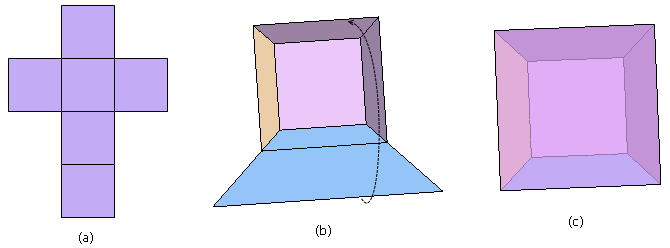
黄色(1個):移動前の立方体 緑色(6個):正方形が移動してできた立方体 青色(1個):移動後の立方体 立方体の展開図と見比べると、この4次元超立方体の形を思い浮かべられるようになるかもしれません。 つぎは、最後の画面です。4次元超立方体を工作します. Dimensionsの第4章見て、 細かくて見えない所を脳内補完して描いた結果がこれだよ。 背景:外側の正八面体(以下、外側) レイヤ1:中間の立方八面体(以下、中間)の手前側 レイヤ2:中間の奥側 レイヤ3:外側と中間を結ぶ線. 主人公クーパーが、無数の立方体が幾重にも折り重なった 4次元超立方体テサラクトの空間 に辿り着いたシーンです。そこは、娘マーフの部屋を通じて 地球の過去、現在、未来全ての時間と連結している空間 であると気付きます。「縦の糸はあなた、横の.
>4次元超立方体の展開図は理屈上は3次元になるんでしょうが、3次元住民には元の形がわからないので、 同様の議論が発生するのです。 横から見て みたいに一直線に立方体が並んでる「展開図」は、正8包体の正しい展開図ではないのです。. 本記事では準モンテカルロ法(Quasi-Monte Carlo, QMC)というアルゴリズムを紹介します。 準モンテカルロ法は、高次元の超立方体$0,1^s$上の関数を数値的に積分するためのアルゴリズムです。. 超立方体(ちょうりっぽうたい、hypercube)とは、2次元の正方形、3次元の立方体、4次元の正八胞体を各次元に一般化した正多胞体である。 なお、0次元超立方体は点、1次元超立方体は線分である。 正測体(せいそくたい)、γ体(ガンマたい)とも言い、n 次元超立方体を と書く。.
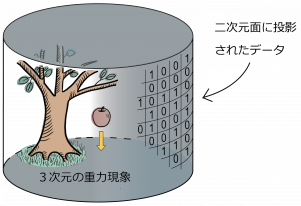
「4次元や5次元の世界に行く」という考え方自体が間違えているように思います。 この3次元空間である宇宙空間は、太陽などのように質量がものすごく大きな天体の近くでは4次元方向に空間が歪んでいることが観測されています。 上の図は、地球と月の周囲の空間の歪みを模式的に表したもの. 2.7 多胞体・超曲面 2box 4次元問答 3章_多胞体 3.1 多角形・多面体・多胞体 3.2 4次元立方体 3.3 4次元立方体の投影 3.4 4次元立方体の回転 3.5 4次元立方体の切断 3.6 4次元立方体の展開 3.7 超角柱・超角錐 3.8 超反角柱. 4 次元の超立方体は3 次元的な超面すなわちここでは 立方体でおおわれていた。 そこでは毛細管網に相当するものが3 次元超シートに 沿って存在するはずである。 3 次元的に拡がった毛細管網とはどんなものであろ うか。.
頂点が原点で,辺が 軸上に有る単位立方xyzu 体の から最も遠い点は で, は対角線のつとなる この立方体を が を通るように平面 上で 回転させ超平面 上に直投影すると 辺が. 11次元宇宙の話は別の機会にするとして、まずは4次元空間を図示してみましょう。 最後の1枚、いかがでしょうか。8つの立方体をうまくたたむと、4次元の超立方体ができます。 例えばこちら(答え)です。答えを見ても図示だけでは納得しづらい問題なの. こんにちは、株式会社CFlatです。前回は下図のように4次元超立方体を2次元ディスプレイに表示しました。 今回は4次元超立方体を回転させてみます。 zw平面で回転 次元がいくつ増えても、ある平面を回転するだけなら回転行列の算出は難しくありません。 下図のようにx = 0, y = 0のzw平面上で.
4次元空間の正多胞体(regular polytope)の分類 シュレフリー記号 3-セル 頂点数 正5胞体 {3, 3, 3} 正4面体 5 正8胞体 {4, 3, 3} 立方体. 超立方体の「標準的な直投影」 A,,, A g(1,1,1,1) Ag 1 .,Ag E(0,0,1,0) OgE, z=0 , 1 3/2 12. Cabri3Dのplugin(無料) はここから ダウンロードできます.Cabri3Dのソフト(有料)はここから購入できます.一ヶ月の試用も出来ます.Cabri図は,画面上でクリックすればマウスでいろいろ操作できます..
たとえば、立方体の影を平面に斜めに映して2次元にすると正方形にならず、 角が直角になっていません。 同じように、4次元の立方体(超立方体)の影(?)を空間に斜めに映して3次元にすると立方体にならず、 角が直角になっていません。. アイ「立方体の中に内接する球を考えるんですね.この ときも球は直方体を埋められていると思いますよ.」 サイ「さすが,アイくん.話が早いね.じゃあ,頭のな かにイメージできなくなるけど,4次元,5次元・・・・・・. 4次元の立方体(超立方体)ができるはずです。 これを、4次元の立方体、つまり 超立方体 ということにしましょう。 (色のつけ方ひとつで、ずいぶんとちがって見えるものですね。.
先ほど超立方体を8個の胞に分解しましたが,先ほどの超立方体の作り方によれば,これらの辺はすべて垂直で,また辺の長さはすべて だったのですから,8個ともすべて の立方体なのです。それらが立方体に見えないのは,次元を落として描いているために. この記事は数値計算 Advent Calendar 18の4日目の記事です。.
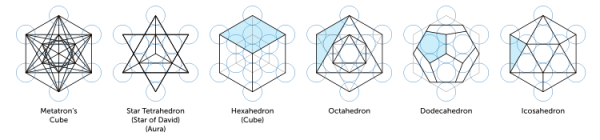
17 5 15 梅塔特隆立方體 寶瓶世紀聖哲曼學院 痞客邦
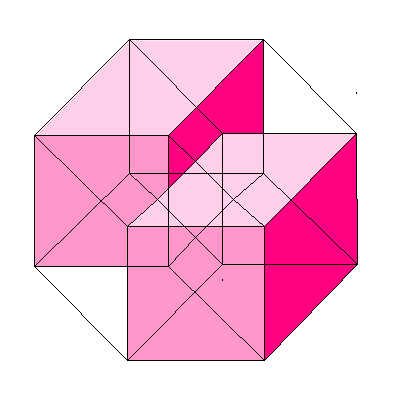
グラフ さんすう 数学のお勉強
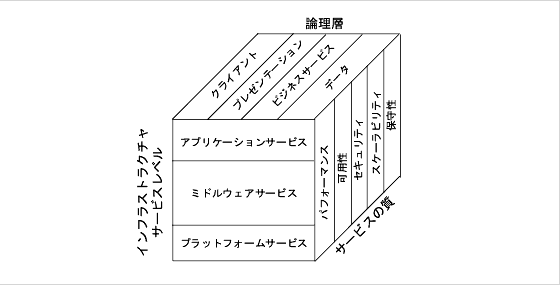
第 2 章 Java Enterprise System のアーキテクチャ
4次元超立方体 のギャラリー

U4qheq1ynpgkhm

超ひも理論とは この世界は11次元である 万物の理論 リアイム

图解 什么是超级立方体 异次元杀阵吧 百度贴吧

數學的浪漫 上
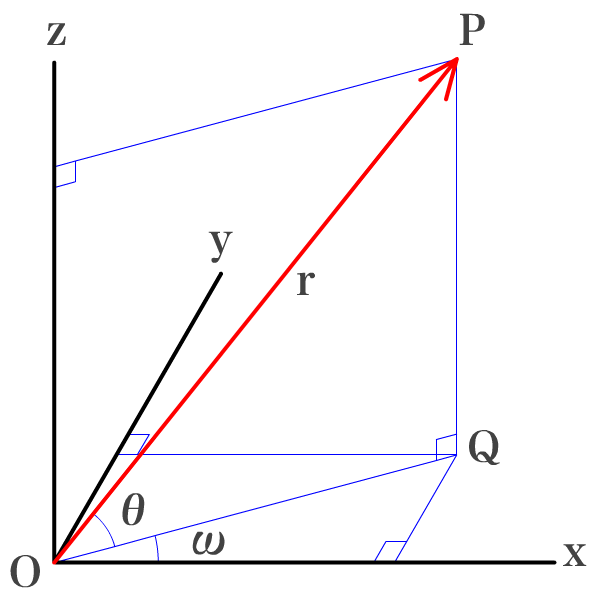
Away3d Typescriptではじめる3次元表現 13 パーティクルを炎のように表現する Gihyo Jp

头条文章

Vs テセラック 佐藤日記 第六部 最終章

一共有多少个维度 每个维度各是什么意思 知乎

四维空间 Wikiwand

4次元超立方体の角 その1 Beat Angels
2次元と4次元を科学する

ポリトープについて ポリトープ株式会社
一共有多少个维度 每个维度各是什么意思 知乎

超立方体のイラスト かわいいフリー素材集 いらすとや
Collo97
Q Tbn 3aand9gcsrj1dvp4o2h5 6ch2ercanx51u5thlzjetjq Usqp Cau

饕餮天下 What S Life Without Whimsy
cks ブックス 4次元立方体の開き方

Anne Rebirth Anne

Q Tbn 3aand9gcrc Ga1caeqhrkuomyaqssjfqhfams4arkbwq Usqp Cau

超立方体 Wikipedia

はじパタ全力解説 第1章 はじめに Qiita

フラットランド 四次元の世界 そして相対性理論 なおきのブログ

介电质 北城百科网
宇宙への旅人 時空
不同维度的对话 带你进入四维世界 Matrix67 The Aha Moments

正八胞体 Wikiwand
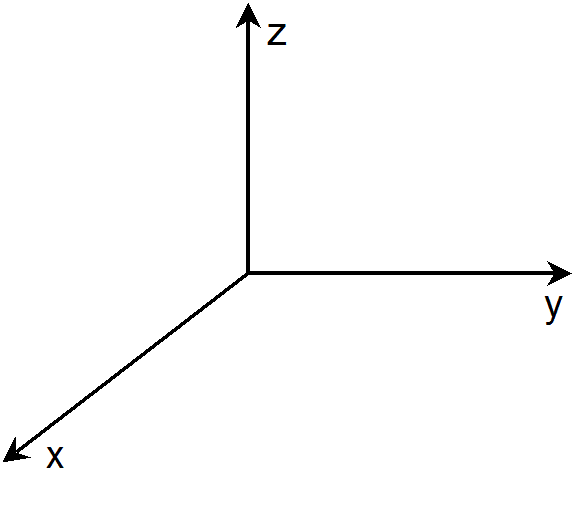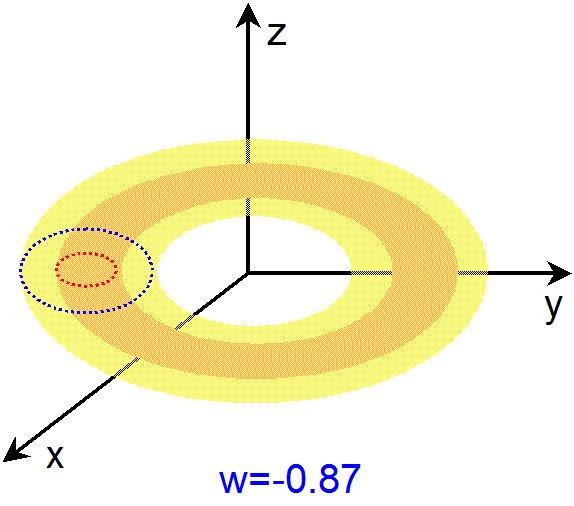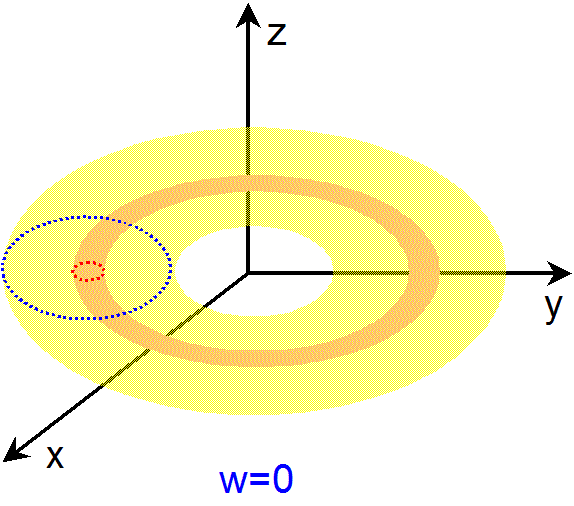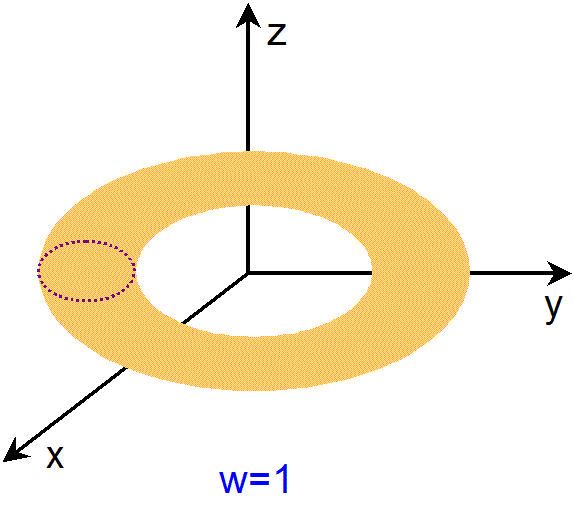
Q Tbn 3aand9gcs1ujvc6kkdqdno Ok9q4ihxi4c63z91njo0a Usqp Cau

中学数学 空間図形
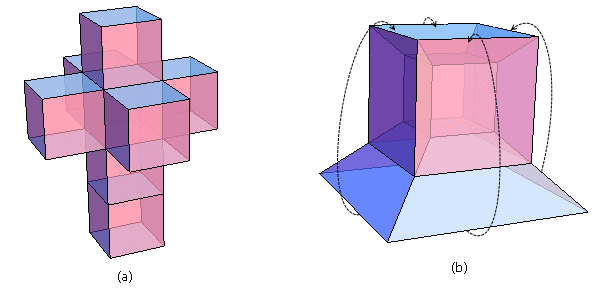
不同维度的对话 带你进入四维世界 Matrix67 The Aha Moments

料理次元 馄饨 萌娘百科万物皆可萌的百科全书
科学入佛学系列 宇宙维度戏论 从霍金时间简史看佛法 自由微信 Freewechat
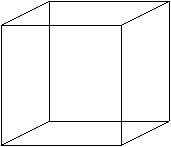
4次元の立方体を描く
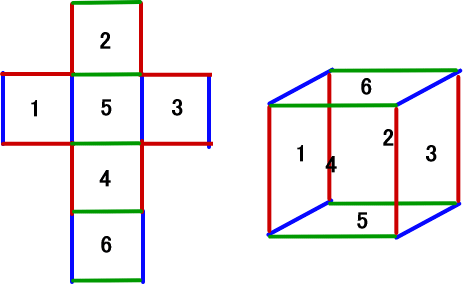
シュタイナーの四次元その14 シュタイナーから読み解く神秘学入門 楽天ブログ

正八胞体 Span Class B Floatr Exp Img Downimg B Hide Span Span Class B Floatr Exp Img Upimg Span Div Class Datavc Div Class B Vpanel B Divsec Div Class B Mtext 概要 Div Div Div Div Div Div Div Class Acc Wrapper Data Priority 2 Div
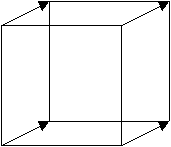
4次元の立方体を描く

Knznymmmy Code777 4d を読んだ

万字干货 21 体验设计趋势报告 人人都是设计师
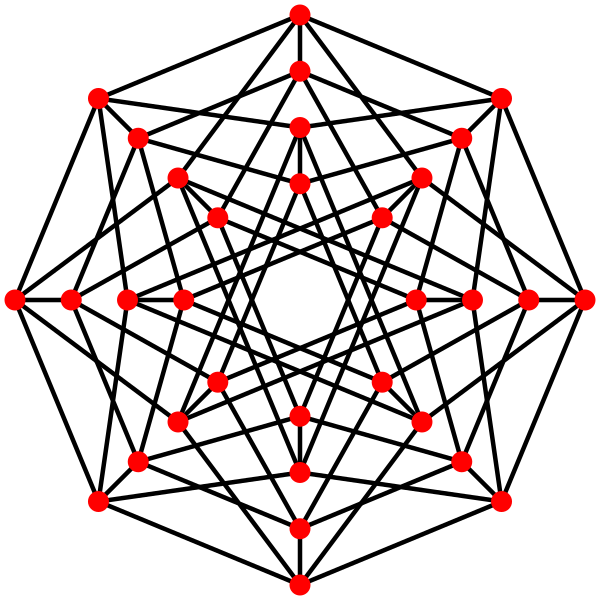
图解 什么是超级立方体 异次元杀阵吧 百度贴吧

立方體 幾何圖形 定義 立方體特徵 幾何性質 聯繫 套用 日常生活 遊戲 視錯覺 中文百科全書
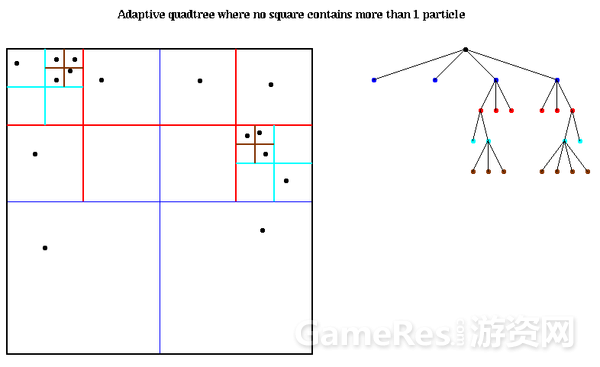
干货分享 游戏场景管理的八叉树算法解析 It S Time Csdn博客

四維超正方體 维基百科 自由的百科全书
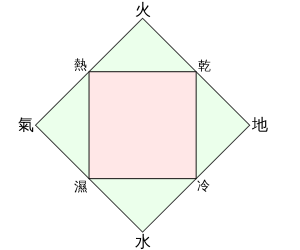
入門 古埃及女祭司的靈魂旅程 7 網上導讀會 宇宙的奧秘 30 35章 怡然之光 新浪博客

cks ブックス 4次元立方体の開き方
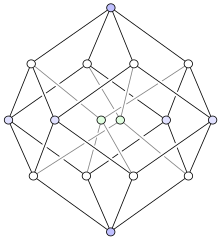
この記事は検証可能な参考文献や出典が全く示されていないか 不十分です 出典を追加して記事の信頼性向上にご協力ください 12年9月 4次元超立方体の3次元投影図 正八胞体 せいはちほうたい または四次元超立方体 8 Cell Octachoron

グラフdbのneo4jで関連キーワード検索を試してみる Visasq Tech Blog

グラフ さんすう 数学のお勉強

申万宏源 潮玩盲盒行业深度报告 潮玩盲盒迅速崛起 玩家共享巨大行业红利 行业分析 慧博投研资讯

四維超正方體 维基百科 自由的百科全书

魂の自分 肉体の自分 そして宇宙の自分 私的な備忘録的な何か
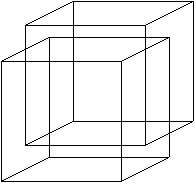
4次元の立方体を描く

正四面体 せいしめんたい の意味や定義 Weblio辞書
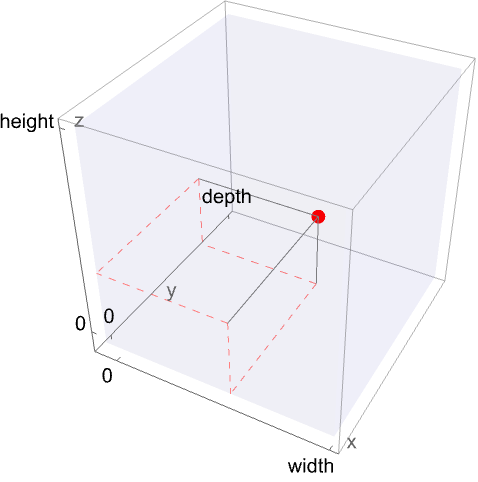
立体描画と処理 Wolfram言語ドキュメント
四次元世界 qazのつれづれ日記

Flatland In Disappear

图解 什么是超级立方体 异次元杀阵吧 百度贴吧

正二十四面体 Www Shianwang Com

四维空间 Wikiwand
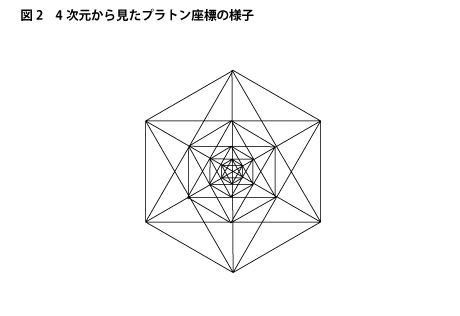
トランスフォーマー型ゲシュタルト ページ 4 Cave Syndrome

申万宏源 潮玩盲盒行业深度报告 潮玩盲盒迅速崛起 玩家共享巨大行业红利 行业分析 慧博投研资讯

Knznymmmy Code777 4d を読んだ
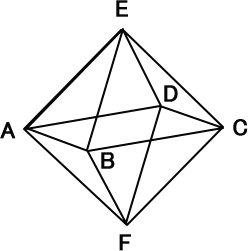
シュタイナーの四次元その17 シュタイナーから読み解く神秘学入門 楽天ブログ
掲示板 シムダンス 四次元能 Beach ビーチ

Q Tbn 3aand9gcsi Fej1wrpt8zkdqfux8qsbrvr0cqcfqbmnq Usqp Cau

ゾムvrmlギャラリー Japan Zome Club

深度学习方法 五 卷积神经网络cnn经典模型整理lenet Alexnet Googlenet Vgg Deep Residual Learning 神经网络算法 电子人社区

不同维度的对话 带你进入四维世界 Matrix67 The Aha Moments

据说18第一网红蛋糕就是它 看完就学会 网易订阅
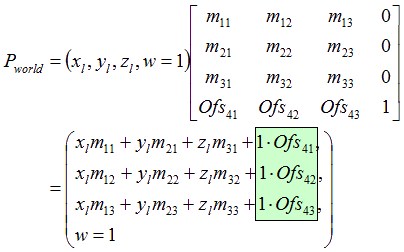
その55 そもそも W って何なのか
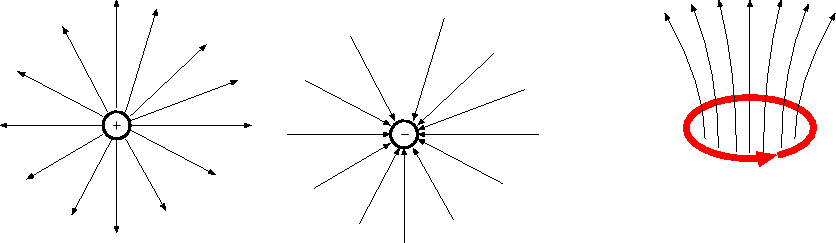
2次元と4次元を科学する
どうしたら四次元を視覚化できるでしょうか Quora

No 029 超立方体ってどんな立体
佑佑佑小溪png素材免抠图漂浮素材几何图形线条立方体几何背景素材

誰かにネガティブになった時はパラダイムシフトの考え方をしてみる 花籠陰陽堂
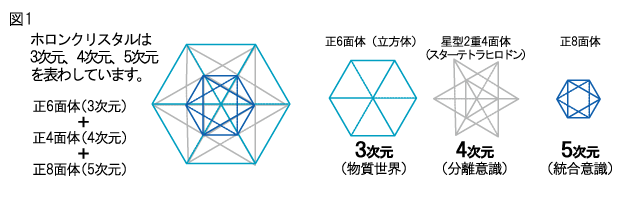
高次元のパワーを生み出す ホロンクリスタル ペンダント スパイラル

Vocalotd 半次元 Acg爱好者社区
高次元とは目に見えない世界ですか 三次元も含むなら一部見えます Yahoo 知恵袋
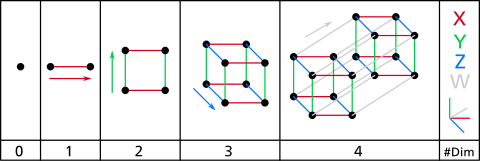
四維超正方體 维基百科 自由的百科全书

超立方体 Wikipedia

据说18第一网红蛋糕就是它 看完就学会 网易订阅

Graphdata Wolfram言語ドキュメント
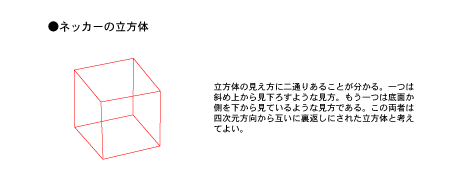
差異と反復 7 Cave Syndrome

4次元立方体 それぞれの軸に対応する辺の色分け Ginjilism Note
Miurror Makoto Miura Github

位相幾何学的グラフ理論
骗 炮 傻 老 外 图 鉴 X博士 二十次幂
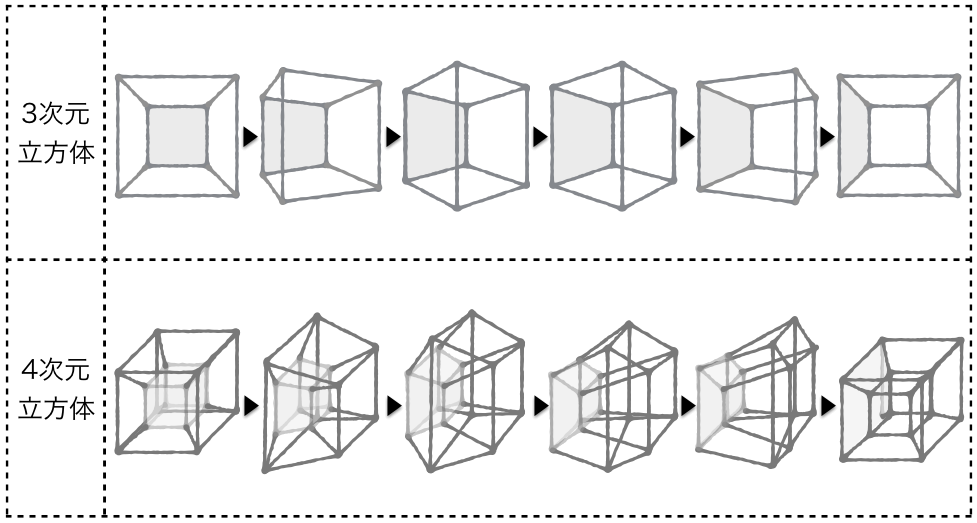
cks ブックス 4次元立方体の開き方
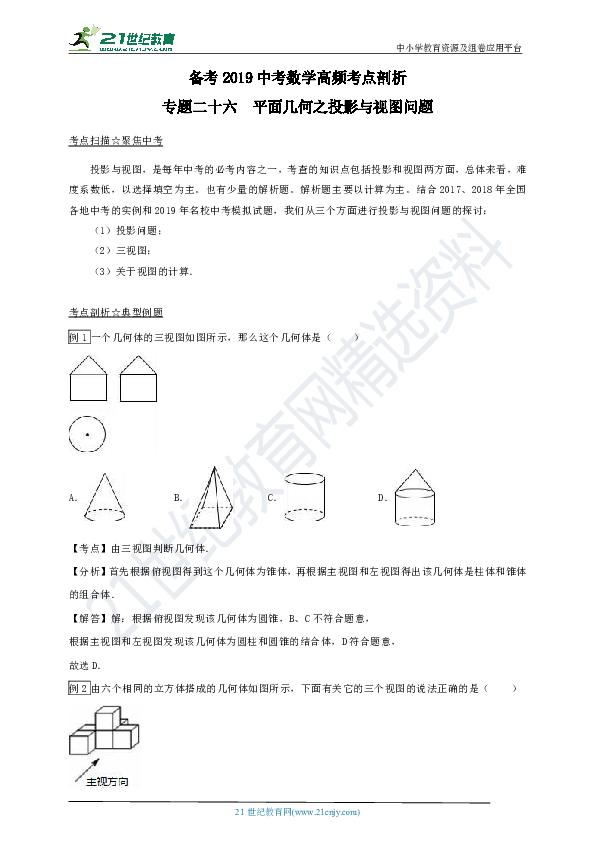
平面几何投影 什么是平面几何投影 点到平面上的投影 点在平面的投影

第一章 宇宙の構造

超立方体について 緑茶思考ブログ

4次元超立方体の角 その1 Beat Angels
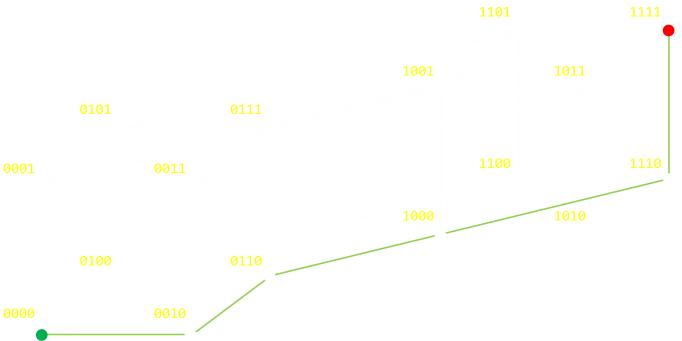
ハミング符号 データの誤り検知 訂正をインタラクティブに学ぶ Postd
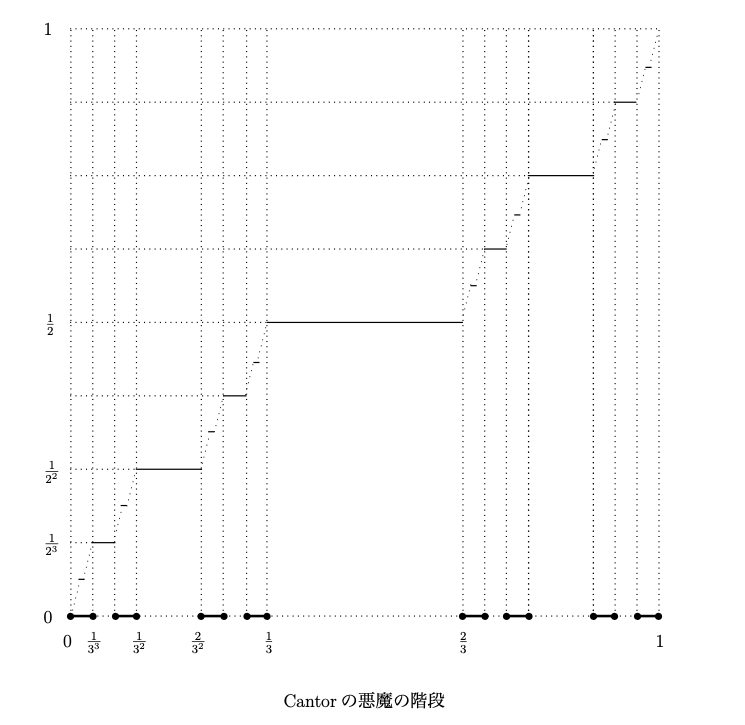
不思議な連続写像たち 応用数理学科 小山晃 早稲田大学 基幹理工学部 研究科

从 星空 主题绘画系统出发寻求绘画的可能性 Weixin 的博客 Csdn博客
最大数之父 葛立恒逝世 这位世纪数学巨匠 也是位杂技演员 Acfun弹幕视频网 认真你就输啦 W ノ つロ
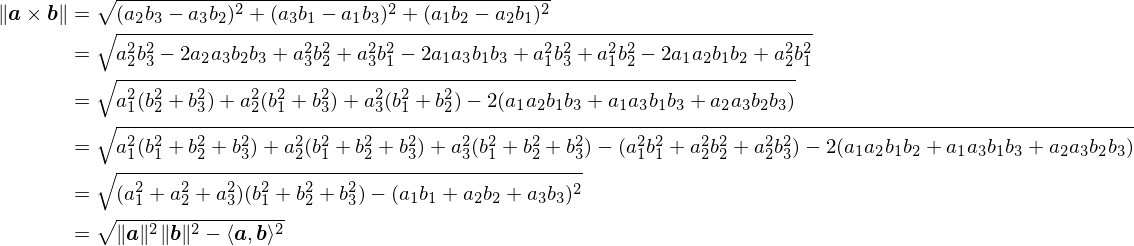
行列式は計量であるという話 Noppoman Note
佑佑佑小溪png素材免抠图漂浮素材几何图形线条立方体科技背景素材




